This page contains the personal projects that I have worked on recently, split into categories based on the type of project.
Publications
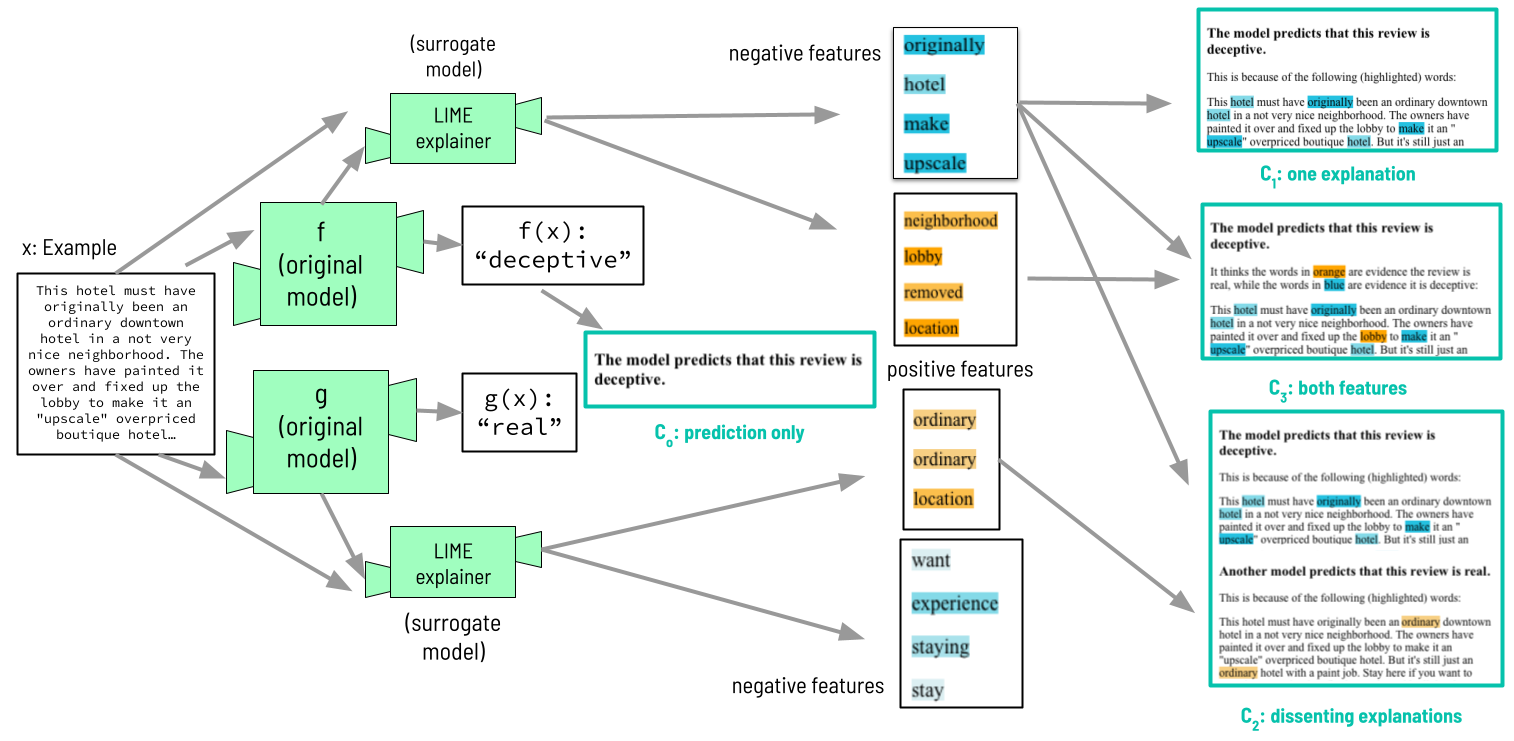
Dissenting Explanations
This paper provides a new framework for viewing explanations as arguments supporting different model predictions, rather than proofs that such predictions are correct. We provide user studies to show that in the case where we want humans to learn from AI explanations while making the final decision, providing dissenting explanations generated from models making opposing predictions allows them to significantly reduce overreliance on the original model, without significantly reducing accuracy. I worked on this project with PhD student Judy Shen, in Omer Reingold's algorithmic fairness lab. It was presented at the AI & HRI workshop at the International Conference on Machine Learning in July 2023.
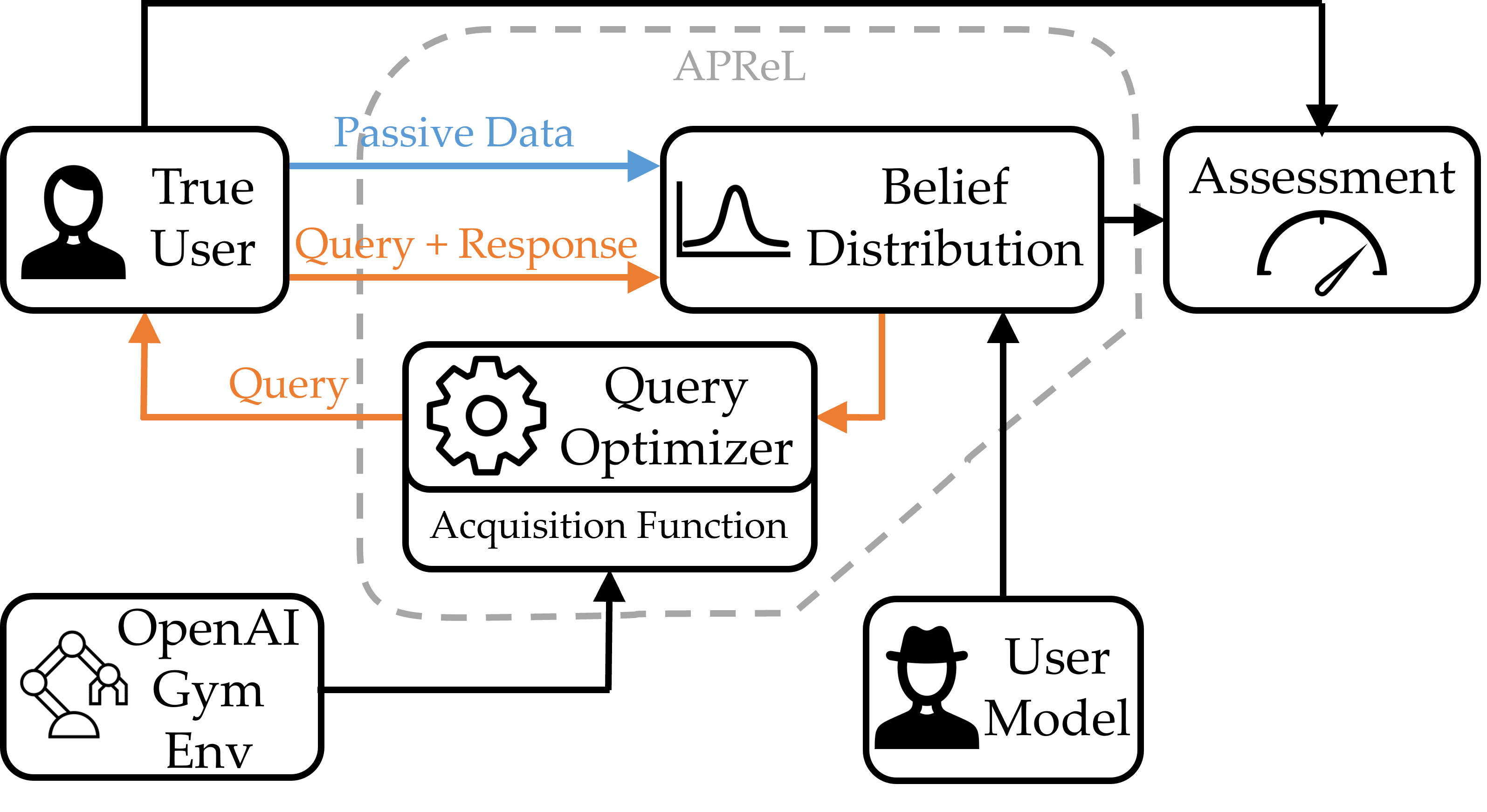
APReL
APReL, or A Library for Active Preference-based Reinforcement Learning Algorithms, is a library of different methods of generating informative, easy-to-answer queries for a learning agent to ask an expert for the sake of reinforcement learning. I worked on this project under PhD student Erdem Bıyık, and the related paper was presented at the ACM/IEEE International Conference on Human-Robot Interaction (HRI) in March 2022.
PantheonRL
PantheonRL is a platform for dynamic multi-agent training interactions, allowing users to easily create environments in which they can train learning agents that are meant to adapt to changing partners in multi-agent situations. I worked on this project with Bidipta Sarkar under PhD student Andy Shih, and the related paper was presented in the demo track of the AAAI Conference on Artificial Intelligence in February 2022.
Class Projects
FirePOMDP
In this paper, we model the spread of wildfires as a partially-observable Markov decision process, where a wildfire starts in some cells of a grid world and then spreads as a random variable according to factors such as wind. We assume that firefighters have limited resources in terms of putting out fires, and that some cells, representing residential areas, are more important to protect than others, and then use POMDP solver methods to learn the optimal way to fight the fire and limit spread. This was a final project for CS 238: Decision Making under Uncertainty.

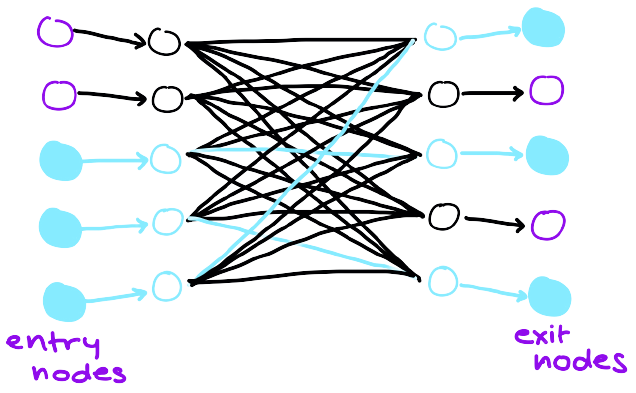
Super-Duper Concentrators and the Pebble Game
The above paper is about the Pebble Game, which is a game played on graphs that is useful to understanding space complexity bounds on Turing machines. In the paper, I describe the construction of a family of graphs called super-duper concentrators, and prove that these graphs are difficult to pebble. If you know a bit of graph theory and know the Pigeonhole Principle, the paper should be easy to follow. This was a final project for CS 254b: Computational Complexity II.
Deep Equilibrium Models
In this paper, we investigate the properties of deep equlibrium models, a type of recursive neural network where multiple hidden layers are replaced by a singular differential equation, which effectively repeats the hidden layer until a fixed point of the differential equation is found. Deep equlibrium models are a useful method of improving memory constraints on neural networks, because they achieve the performance of a many-layer network while only requiring a singular layer of parameters to be stored. In this paper, we apply DEQs to the simple sequential decision-making task of reading and solving arithmetic equations, and find that the DEQ model is able to achieve similar performance to a multi-layer GRU-based network, even when our differential equation solver is unable to find a true fixed point of our implicit layers. This was a final project for CS 229: Machine Learning and won best project for the class.

Paper on the Hausdorff Dimension
This is a paper that I wrote as a final project for a class. It is an expository paper on fractals and how to measure them, specifically using the Hausdorff measure to show the way in which fractals have a fractional dimension. Then, the paper moves on to discussing Peano curves and why space-filling curves are cool. This assumes some background knowledge on measure theory, specifically about the Lebesgue measure.
Other
Problem-Set Template
This is an Overleaf template that I have created to help myself and others easily type up pretty LaTeX-ed solutions to homework problem sets. It uses custom problem and solution commands that are defined in a package I created, and has custom commands that are regularly updated as I find more creative formatting tools. An explanation on how to use the template is in the comments of psetTemplate.tex, and to make a copy of the template to use for your own problem set, simply click the Menu button in the top-left corner, and then "Copy Project."
Contact me